KenKen Parity Strategy
The first discussion of the Parity Strategy found so far is in 2010 by Tom Davis. Separately in a 2011 paper by Reiter, Thornton and Vennebush. I am grateful to Roger Taft for finding these, composing much of this article and sending examples found from solving KenKen puzzles. As of 1st February 2025 the full Parity Strategy implementation is in the KenKen solver. Should be a powerful tool on the hardest puzzles. Looking at you New York Times. (Ed.)
Parity is easy to check for. When other strategies have been exhausted, there is a good chance an advance based on parity is possible. That advance usually solves the whole puzzle.
Take this very simple situation of a single row in a 6x6 KenKen. We know that the whole row must add up to 21, an ODD number. The two cages with -1 must have values that add up to an ODD number.
 Two ODDs make an EVEN therefore the final unknown cage must be ODD to fit with the whole row being ODD.
Two ODDs make an EVEN therefore the final unknown cage must be ODD to fit with the whole row being ODD.
The possible values of that 12x cage are: {2,6} and {3,4}. {2,6} sums to 8 which is EVEN and is ruled out. {3,4} sums to 7 which is ODD and so must be the values for that cage.
Parity is easy to check for. When other strategies have been exhausted, there is a good chance an advance based on parity is possible. That advance usually solves the whole puzzle.
Take this very simple situation of a single row in a 6x6 KenKen. We know that the whole row must add up to 21, an ODD number. The two cages with -1 must have values that add up to an ODD number.

The possible values of that 12x cage are: {2,6} and {3,4}. {2,6} sums to 8 which is EVEN and is ruled out. {3,4} sums to 7 which is ODD and so must be the values for that cage.
Determining Cage Parity
First, some terminology. A KenKen board is a 6x6 square grid of cells. Adjacent rows (or columns) can be grouped together as a block. Within a block there are cages, a set of contiguous cells, with an associated arithmetic operation (add, subtract, multiply, divide) and a target value. The cages may be complete (wholly inside the black) or partial (where the cage is crossed by a block boundary).
Parity is the mathematical property of being ODD or EVEN. The odd numbers, 1, 3, 5 … have odd parity. The even numbers 2, 4, 6 … have even parity. The sum of two odd numbers is even so has even parity. A set of odd numbers has the parity of the count of the number of items in the set. Each row or column in the board sums to 21 (giving rise to the “Rule of 21”) so has odd parity. A block has the parity of the width of the block. So a block 2 rows wide has EVEN parity as does the whole board.
Each cage or partial cage in a block has a parity. The parity strategy looks for a block where each cage (complete or partial) has a known parity except exactly one. Since the parity of the block is known, the parity of the single unknown cage becomes known. This new information is used to advance the solution.
The parity of a block is the parity of the block width: blocks 1, 3, and 5 wide have ODD parity, blocks 2, 4, and 6 (the whole puzzle) have EVEN parity.
The Parity Rule is: Find a block where all cages (complete and partial) have known parity except for a single cage (complete or partial). Then the parity of the unknown cage is:
Parity is the mathematical property of being ODD or EVEN. The odd numbers, 1, 3, 5 … have odd parity. The even numbers 2, 4, 6 … have even parity. The sum of two odd numbers is even so has even parity. A set of odd numbers has the parity of the count of the number of items in the set. Each row or column in the board sums to 21 (giving rise to the “Rule of 21”) so has odd parity. A block has the parity of the width of the block. So a block 2 rows wide has EVEN parity as does the whole board.
Each cage or partial cage in a block has a parity. The parity strategy looks for a block where each cage (complete or partial) has a known parity except exactly one. Since the parity of the block is known, the parity of the single unknown cage becomes known. This new information is used to advance the solution.
The parity of a block is the parity of the block width: blocks 1, 3, and 5 wide have ODD parity, blocks 2, 4, and 6 (the whole puzzle) have EVEN parity.
The Parity Rule is: Find a block where all cages (complete and partial) have known parity except for a single cage (complete or partial). Then the parity of the unknown cage is:
| Block Parity | Known Cage Parity | Unknown Cage Parity |
| EVEN | EVEN | EVEN |
| ODD | ODD | |
| ODD | EVEN | ODD |
| ODD | EVEN |
Unknown Cage Example
Pairs of rows or columns add up to 42, an EVEN number.
Columns 5 and 6 (blue rectangle) wholly enclose three cages.
The top cage starting on A5 is 15+ so ODD. The bottom cage starting on E5 is 14+ so EVEN.
Load This example.
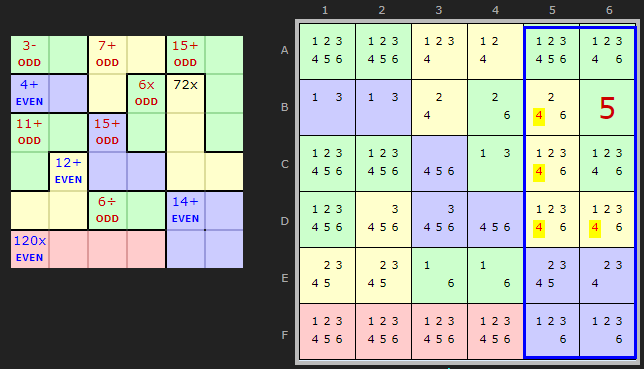
The one remaining cage starting on B4 is our target. To determine the parity of the whole block, exclusive of the target cage, we simply count the number of odd parity elements and note the parity of the count. In this case there is one odd so the aggregate is ODD, meaning the target must be ODD.
A 72x in a four-cage with 'dog-leg' cells implies these solutions as seen in the cage hover:
2x3x3x4 = 72 which is 2+3+3+4 = 12 EVEN
2x2x3x6 = 72 which is 2+2+3+6 = 13 ODD
1x3x4x4 = 72 which is 1+3+3+4 = 13 ODD
1x2x6x6 = 72 which is 1+2+6+6 = 15 ODD
The first option is EVEN so we can discard it.
The third option is not possible given the remaining candidates in the cells.
If those two options are discarded there is no place for a 4 in the cage.
Note: In this example the block value is 42 which is EVEN. So it does not contribute to the parity count. Whereas the single row example we started with sums to 21 - which is ODD and so it included in the count of elements.
We could also consider the whole board. It contains seven ODD cages confirming the one unknown cage is ODD as well.
Columns 5 and 6 (blue rectangle) wholly enclose three cages.
The top cage starting on A5 is 15+ so ODD. The bottom cage starting on E5 is 14+ so EVEN.
Load This example.

The one remaining cage starting on B4 is our target. To determine the parity of the whole block, exclusive of the target cage, we simply count the number of odd parity elements and note the parity of the count. In this case there is one odd so the aggregate is ODD, meaning the target must be ODD.
A 72x in a four-cage with 'dog-leg' cells implies these solutions as seen in the cage hover:
2x3x3x4 = 72 which is 2+3+3+4 = 12 EVEN
2x2x3x6 = 72 which is 2+2+3+6 = 13 ODD
1x3x4x4 = 72 which is 1+3+3+4 = 13 ODD
1x2x6x6 = 72 which is 1+2+6+6 = 15 ODD
The first option is EVEN so we can discard it.
The third option is not possible given the remaining candidates in the cells.
If those two options are discarded there is no place for a 4 in the cage.
Note: In this example the block value is 42 which is EVEN. So it does not contribute to the parity count. Whereas the single row example we started with sums to 21 - which is ODD and so it included in the count of elements.
We could also consider the whole board. It contains seven ODD cages confirming the one unknown cage is ODD as well.
Common Parity Cases
The parity of a complete cage depends on the operation and target value. Here are the parities of the common cases:
Cage Operation Plus or Minus. Parity of the target value.
For example, the parity of a cage with a 1- operation is ODD.
Cage Operation Division. There are only 5 total cases:
2 = 6/3 = 4/2 = 2/1 UNKNOWN
3 = 3/1 = 6/2 EVEN
4 = 4/1 ODD
5 = 5/1 EVEN
6 = 6/1 ODD
Cage Operation Multiply
- see below
The parity of a partial cage is:
Cage Operation Plus or Minus. Parity of the target value.
For example, the parity of a cage with a 1- operation is ODD.
Cage Operation Division. There are only 5 total cases:
2 = 6/3 = 4/2 = 2/1 UNKNOWN
3 = 3/1 = 6/2 EVEN
4 = 4/1 ODD
5 = 5/1 EVEN
6 = 6/1 ODD
Cage Operation Multiply
- see below
The parity of a partial cage is:
- Partial Cage, One Cell, Solved: Parity of solved cell
- Partial Cage, One Cell, All Values Same Parity: Common parity
- Partial Cage, Two Cell Pair: Parity of pair
- Partial Cage, Three Cell Triple: Parity of triple
Having determined the parity of the unknown cage, some reduction in that cage is usually possible. The common cases are:
- Cell Value Now Known. Set cell to the value.
- Cell Parity Now Known. Eliminate numbers of the other parity from the cell.
- Cage Parity Now Known, Two Solutions. Set cage to the valid solution.
- Cage Parity Now Known, Three Solutions. Examine invalid solutions for values that do not appear in the valid solutions and eliminate those values. For example, a cage with the clue 2/ has the possible solutions: {1,2}, {2,4}, {3,6}. If the cage is determined to have even parity the cage is {2,4}; if the cage is determined to have odd parity all 4s can be eliminated
Example 2
This example is taken from KenKen 40924 targets the one cage inside the block with an unknown parity. It is almost the reverse of the first example in that the innie D6 has a known parity but one internal cage is unknown.
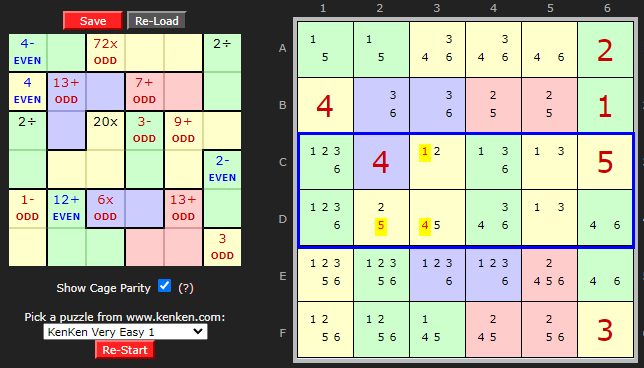
The Rows C+D must add up to 42, so EVEN
Cage C1 (2÷) remaining solutions {1,2} and 3,6} both ODD
Cell C2 (4) EVEN
Cage C3 (20x) UNKNOWN
Cage C4 (3-) ODD
Cage C5 (9+) ODD
Cell D6 = {4,6} EVEN
So unknown cage C3 (20x) must be ODD
A 3-cell cage with 20x has possible values of {1,4,5} EVEN or {2,2,5} ODD so the eventual solution must be the latter.

The Rows C+D must add up to 42, so EVEN
Cage C1 (2÷) remaining solutions {1,2} and 3,6} both ODD
Cell C2 (4) EVEN
Cage C3 (20x) UNKNOWN
Cage C4 (3-) ODD
Cage C5 (9+) ODD
Cell D6 = {4,6} EVEN
So unknown cage C3 (20x) must be ODD
A 3-cell cage with 20x has possible values of {1,4,5} EVEN or {2,2,5} ODD so the eventual solution must be the latter.
Parity Value for Common Multiply Cases
| 4 (2 cell) | = 1*4 | ODD |
| 4 (3 cell) | = 1*1*4 = 1*2*2 | UNKNOWN |
| 6 (2 cell) | = 1*6 = 2*3 | ODD |
| 6 (3 cell) | = 1*1*6 = 1*2*3 | EVEN |
| 8 (2 cell) | = 2*4 | EVEN |
| 8 (3 cell) | = 1*2*4 | ODD |
| 9 (3 cell) | = 1*3*3 | ODD |
| 10 (2 cell) | = 2*5 | ODD |
| 10 (3 cell) | = 1*2*5 | EVEN |
| 12 (2 cell) | = 2*6 = 3*4 | UNKNOWN |
| 12 (3 cell) | = 1*2*6 = 1*3*4 = 2*2*3 | UNKNOWN |
| 15 (2 cell) | = 3*5 | EVEN |
| 15 (3 cell) | = 1*3*5 | ODD |
| 16 (3 cell) | =1*4*4 = 2*2*4 | UNKNOWN |
| 18 (2 cell) | = 3*6 | ODD |
| 18 (3 cell) | = 1*3*6 = 2*3*3 | EVEN |
| 20 (2 cell) | = 4*5 | ODD |
| 20 (3 cell) | = 1*4*5 = 2*2*5 | UNKNOWN |
| 24 (2 cell) | = 4*6 | EVEN |
| 24 (3 cell) | = 1*4*6 = 2*2*6 = 2*3*4 | UNKNOWN |
| 25 (3 cell) | = 1*5*5 | ODD |
| 30 (2 cell) | = 5*6 | ODD |
| 30 (3 cell) | = 1*5*6 = 2*3*5 | EVEN |
| 32 (3 cell) | = 2*4*4 | EVEN |
| 36 (3 cell) | = 1*6*6 = 2*3*6 = 3*3*4 | UNKNOWN |
| 40 (3 cell) | = 2*4*5 | ODD |
| 45 (3 cell) | = 3*3*5 | ODD |
| 48 (3 cell) | = 2*4*6 = 3*4*4 | UNKNOWN |
| 48 (4 cell) | = 1*2*4*6 = 2*2*3*4 | ODD |
| 50 (3 cell) | = 2*5*5 | EVEN |
| 50 (4 cell) | = 1*2*5*5 | ODD |
| 54 (3 cell) | = 3*3*6 | EVEN |
| 60 (3 cell) | = 2*5*6 = 3*4*5 | UNKNOWN |
| 60 (4 cell) | = 1*2*5*6 = 1*3*4*5 = 2*2*3*5 | UNKNOWN |
| 72 (3 cell, straight) | = 3*4*6 | ODD |
| 72 (3 cell, bent) | = 2*6*6 = 3*4*6 | UNKNOWN |
| 75 (3 cell) | = 3*5*5 | ODD |
| 80 (3 cell) | = 4*4*5 | ODD |
| 90 (3 cell) | = 3*5*6 | EVEN |
| 96 (3 cell) | = 4*4*6 | EVEN |
| 100 (3 cell) | = 4*5*5 | EVEN |
| 108 (3 cell) | = 3*6*6 | ODD |
| 120 (3 cell) | = 4*5*6 | ODD |
| 120 (4 cell) | = 1*4*5*6 = 2*2*5*6 = 2*3*4*5 | UNKNOWN |
| 144 (3 cell) | = 4*6*6 | EVEN |
| 150 (3 cell) | = 5*5*6 | EVEN |
| 180 (3 cell) | = 5*6*6 | ODD |
| 216 (4 cell) | = 2*3*6*6 = 3*3*4*6 | UNKNOWN |
| 288 (4 cell) | = 2*4*6*6 = 3*4*4*6 | UNKNOWN |
| 288 (5 cell) | = 2*2*3*4*6 | ODD |
Example 3 - Whole Board
Good example of a Whole Board parity elimination is this example. We have one cage we can't figure out the parity for and it is a 2÷ - the cage starting on D1.
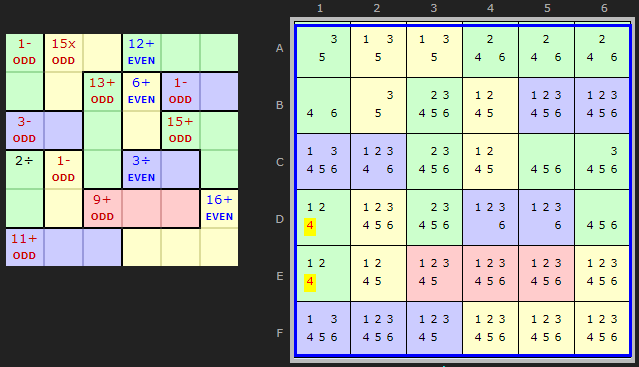
The whole board has EVEN parity (6x21) so doesn't count.
There are 4 cages with EVEN parity.
And there are 9 cages with ODD parity so DE1 must be odd. That excludes {2,4} as solutions. We can remove the 4s.

The whole board has EVEN parity (6x21) so doesn't count.
There are 4 cages with EVEN parity.
And there are 9 cages with ODD parity so DE1 must be odd. That excludes {2,4} as solutions. We can remove the 4s.
Example 4 - Single Row Innie
In Example 3 we have one cage with unknown parity, the red 3-cell cage with 72x as the clue.
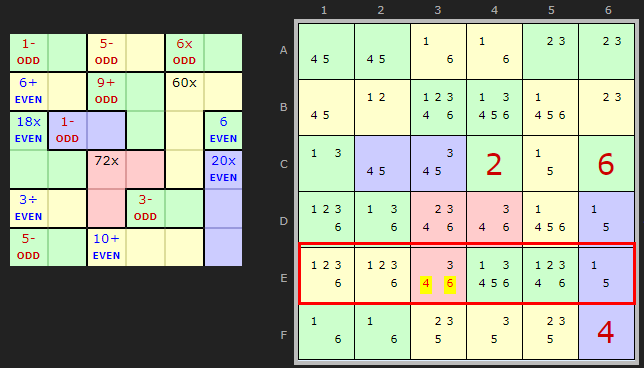
Looking at row E we see there is one EVEN cage and one ODD cage. What about E6? There is a cage straddling the row. We can decide that E6 is odd by looking at the remaining clues 1 and 5. Both are ODD numbers.
Give the row is ODD and E6 is ODD and cage on E4 is ODD we have three ODDs. So the last remaining cell, the innie in E3 must be ODD. That excludes 4 and 6.

Looking at row E we see there is one EVEN cage and one ODD cage. What about E6? There is a cage straddling the row. We can decide that E6 is odd by looking at the remaining clues 1 and 5. Both are ODD numbers.
Give the row is ODD and E6 is ODD and cage on E4 is ODD we have three ODDs. So the last remaining cell, the innie in E3 must be ODD. That excludes 4 and 6.
Example 5 - Two Rows + Innie
Here is a larger 2 row block Innie Example.
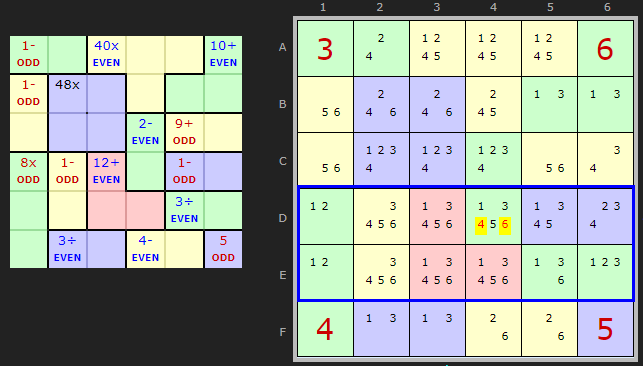
The 3-cell cage on D1 is fortunately partially solved and 'splits' the cage. The remaining two cells in DE1 contain 1 and 2. Together those cells sum to an ODD number.
There are two other cages wholly inside the block which are ODD. Three odds means the innie in D4 must be ODD allowing us to remove 4 and 6.

The 3-cell cage on D1 is fortunately partially solved and 'splits' the cage. The remaining two cells in DE1 contain 1 and 2. Together those cells sum to an ODD number.
There are two other cages wholly inside the block which are ODD. Three odds means the innie in D4 must be ODD allowing us to remove 4 and 6.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Chris
Underneath, it says there are four possible combinations (to get 72x)...
2x3x3x4
2x2x3x6
1x3x4x4 - TWO MISTAKES - this doesn't multiply to 72 and it doesn't have ODD parity!
1x2x6x6
I think the third one needs to be corrected to 1x3x4x6 and given EVEN parity. This would mean it can be discarded, along with the first option, explaining why all the number 4s in the cage can be discarded.
At the moment the explanation is "The third option is not possible given the remaining candidates in the cells" but that's not true - you need to spot the parity is EVEN to get rid of the 4s.
I hope this is useful. It just needs the third option changed to 1x3x4x6, the parity changed to EVEN, then the explanation changed to state the EVEN options can be discarded.
This is a new technique for me so enjoying learning about it, although have not yet got very far into this explanatory page!
Thanks for a brilliant site.