Chute Remote Pairs
Added 24-Jan-2025
This is an excellent and simple pattern we can employ just with eye-balling some cells with the same pair of numbers in them. I've placed it near the start of the 'tough' strategies after X-Wing as it is quite common, doesn't require us to think about strong and weak links, and does not take long to evaluate. Very grateful for Andy Potvin from the United States for promoting the idea to me and sending examples. The idea goes way back and is a break out from W-Wings. I think it is sufficiently distinct to be worth having on it's own but I will be re-evaluating W-Wings soon to see how much they are worth including in their own right.
If you want to see what CRP replaces, untick it and [<<] (back-step) and [Take Step]
All these examples are from tough puzzles and each has two Chute Remote Pairs in them. In testing I've found some 620 examples in 2000 random diabolicals and I've gained an overall speed increase of about 2%. So it is simplifying the solve paths for more than a quarter of puzzles.
This is an excellent and simple pattern we can employ just with eye-balling some cells with the same pair of numbers in them. I've placed it near the start of the 'tough' strategies after X-Wing as it is quite common, doesn't require us to think about strong and weak links, and does not take long to evaluate. Very grateful for Andy Potvin from the United States for promoting the idea to me and sending examples. The idea goes way back and is a break out from W-Wings. I think it is sufficiently distinct to be worth having on it's own but I will be re-evaluating W-Wings soon to see how much they are worth including in their own right.
If you want to see what CRP replaces, untick it and [<<] (back-step) and [Take Step]
All these examples are from tough puzzles and each has two Chute Remote Pairs in them. In testing I've found some 620 examples in 2000 random diabolicals and I've gained an overall speed increase of about 2%. So it is simplifying the solve paths for more than a quarter of puzzles.
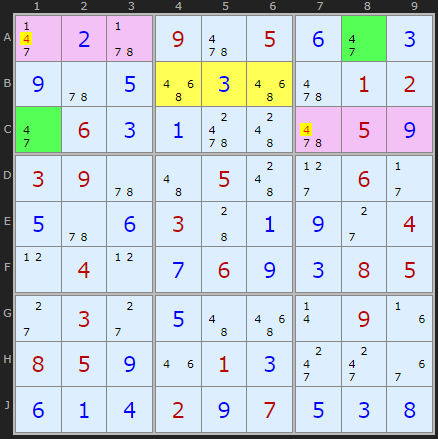
The first example gives the classic pattern. We're looking for two bi-value cells with the same candidates in the same Chute, which is a horizontal or vertical set of the three boxes. There are six chutes in a 9x9 Sudoku.
Both the green cells A8 and C1 here have {4/7}. The next step is to check they can't 'see' each other, ie they are not a Naked Pair but instead a Remote Pair.
Given that pattern there will exist exactly three cells in the unused box in the same chute and I have marked these in yellow {B4, B5, B6).
The rule says,
If the yellow cells have only ONE of the candidates in the green cells then that candidate can be eliminated from all cells seen by both green cells. I've marked these in pink.
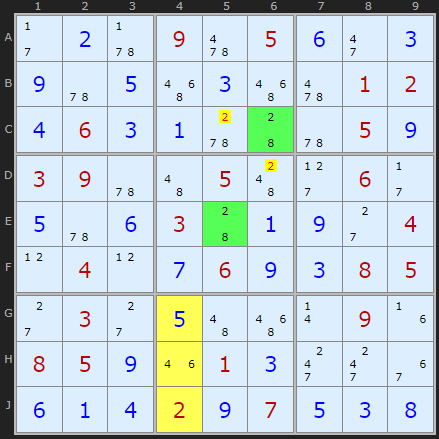
Later on in the puzzle the pattern is found again. We'll try and prove the rule with this second example.
2 and 8 exist in C6 and E5. 2 exists in the third box in J4. Note - it does not matter than this is a clue or solved cell. What is important is the 8 is no where in any of the yellow cells.
If 2 really was the solution to C5 or D6 (the elimination cells) that would force an 8 in both of the green cells. However looking down the column that would remove all 8s from box 8 and we can already see there is no 8 in column 4.
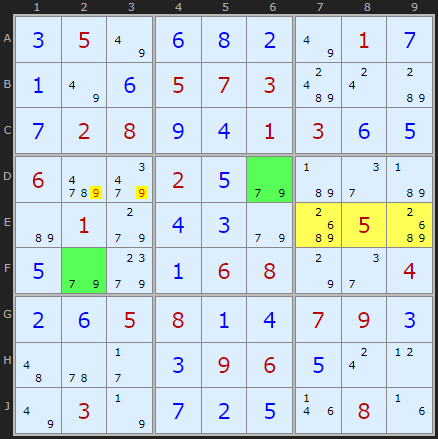
{7,9} in D6 and F2 form a Remote Pair. Looking horizontally along the chute to box 6 we see 9 is present in the yellow cells but 7 is not.
This gives us two eliminations of 9 in D2 and D3. The solver reports:
Chute Remote Pair
7 cannot be set in the yellow cells {E7,E8,E9} and with the Remote Pair in D6 and F2 it means:
9 can be taken off D2
9 can be taken off D3
Double Eliminaton
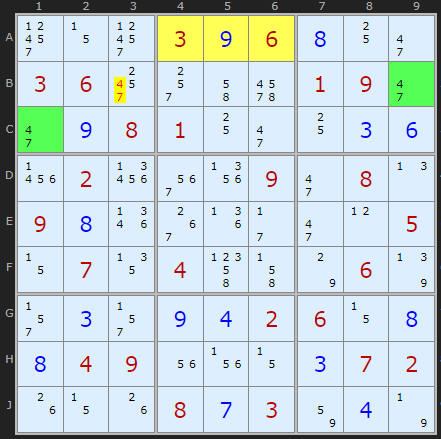
In the final example {4,7} is not present in any of the yellow cells. It is a coincidence this example has all the yellow cells as clues and solved numbers but it makes checking a little easier
We look around for any 4 or 7 that can be seen by B9 AND C1 and B3 fits the bill.
Chute Remote Pair
Neither 4/7 can be set in the yellow cells {A4,A5,A6} and with the Remote Pair in B9 and C1 it means:
4/7 can be taken off B3
Bonus Eliminations
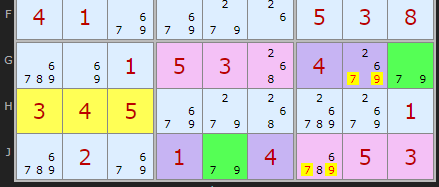
The simple rule is that if one green cell is X the other is Y. And vice versa. This eliminates not just common cells (pink) but in cells the same box as the green cells box and along the row (or column). Check the following:
If J5 is 7, then 7 is removed from J123 thus 7 must be somewhere in G123, and so 7 cannot be in the rest of row G which means G9 is 9
Likewise, if J5 is 9, 9 is removed from J123, so 9 must be somewhere in G123 - so 9 cannot be in the rest of row G which means G9 is 7.
All this is possible because 7 and 9 do NOT appear in the yellow cells.
The solver will report these eliminations with the note 'either end' rule
Neither 7/9 can be set in the yellow cells {H1,H2,H3} and with the Remote Pair in G9 and J5 it means:
7/9 can be taken off J7
7/9 can be taken off G8 ('either end' rule)
7/9 can be taken off J7
7/9 can be taken off G8 ('either end' rule)
Some further testing running 'Ruud's Top 50,000' through the offline solver I get a 1% speed increase - less than 2% because these have so many more AIC searches to do and AIC dwarfs all other strategies in terms of cost. 16,814 CRPs were used in 14,384 puzzles (28.8%) - a lot but there is a bias since CRP benefits from being so close to the top of the strategy ordering. The strategies that reduce the most are Y-Wings (>3k), XY-Chains (2k), 3D Medusa (1k). Simple Colouring and Rectangle Elimination down by only about ~500.
Chute Remote Pair Exemplars
These puzzles require the CRP strategy at some point but are otherwise trivial or have a few other similar level strategies.
They make good practice puzzles.
They make good practice puzzles.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Howard Weiss
with regard to Exemplar 1, I find two other elimation.
In columns 1, 2,3 only F2 and G3 have values 7 and 9, Yellow cells are A1, B1, C1. Only 9 appears in those cells. Cell D3 sees both F2 and G3 and contains a 9 -> eliminate 9 from D3
In columns 7,8,9 only C7 and E9 contain values 5 and 6. Yellow cells are G8, H8, J8. Only 5 appears in those cells. Cell A9 sees both C7 and E9 and contains a 5 -> eliminate 5 in A9
Am I missing something?
Howard Weiss
... by: STRMCKR
http://forum.enjoysudoku.com/two-definitions-of-w-wing-terminology-question-t6452.html
i tried to have you to implement all the named wings/rings of A.I.C methods years ago:
Split wing, L{1,2,3} W, M{2,3}, Hybrid(1,2,3} - Wings / Rings
{single chain}
n X ERi, rec't Kites, dual ER etc
your solver is Niceloops based and struggles to replicate them as many of the named chains have External Eliminations ie not Singular cell{s} contradictions.
where these named as niceloops are DNL inwhich it takes a collection of DNL to replicate the 1 a.i.c.
same applies to A.I.C rings which are replicate in appearance by CNL however they have internal and external Eliminations. Meaning it takes many CNL / or DNL to replicated all the eliminations of the 1 move.
A direct link to how some of the named methods from years past are detected.
http://forum.enjoysudoku.com/named-chains-wings-rings-structure-for-i-ding-in-code-t42435.html
beyond flustered:
http://forum.enjoysudoku.com/post266297.html#p266297
strmckr
... by: nono
... by: Hans Burch