Solver App for Android and iPhone Strategies for Number Puzzles of all kinds
 
Print Version Get the SudokuWiki Newsletter
 
Solvers
Puzzles
Basic Strategies
Tough Strategies
Diabolical Strategies
Extreme Strategies
Depreciated Strategies
Str8ts
Other
The Logic of Sudoku
Order Str8ts Book 1
Order Now!
Order Str8ts Book 2
Order Now!
  Getting Started
Every puzzle from the easiest to the hardest requires simple 'eyeballing' to detect the easy solutions. You certainly need to start the puzzle by checking for simple placements and when you have cracked a puzzle the last ten or twenty cells will fall into place just by letting your eye scan the board. You are looking for any unsolved cell that is the last possible place in a row, column or box for a number to go. There are a number of patterns to look out for.

Last Remaining Cell in a Box

This easy puzzle will demonstrate 'eyeballing'. It is best to start with boxes as they are the easiest shape to work with. Box 7 seems rather crowded with four clues so it's a good bet that some of these cells can be filled quickly. Looking at the 8s on board I can see that the 8 in D3 occupies the whole column and prohibits any 8 in H3 and J3. Likewise the 8 in G5 fills in the whole row preventing any 8 from being placed in G1 and G2.

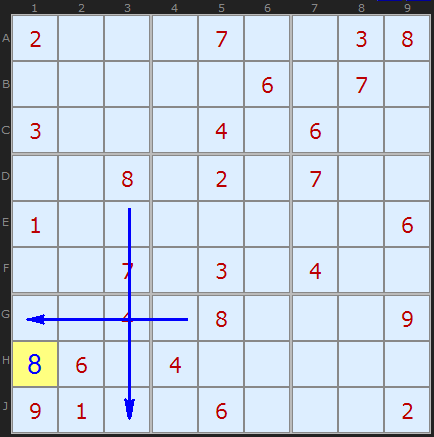
So the last remaining cell in box 7 for an 8 is H1.
 Last number in a Box
Last number in a Box: Load Example
Last Remaining Cell in a Row

When you have scanned the boxes for obvious solutions check the rows and columns. The arrangement of 4s on this board suggest something in the first row, row A. We have a 4 in G3 which occupies the space in A3. Likewise the 4 in F7 removes A7 as a placement for 4. And the 4 in box 2 uses up all the places in A4, A5 and A6.

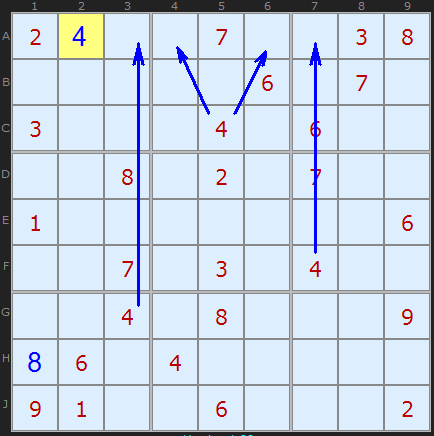
So the last remaining cell for 4 in the row is A2. 		Last number in a row
Last number in a row

Pinned!

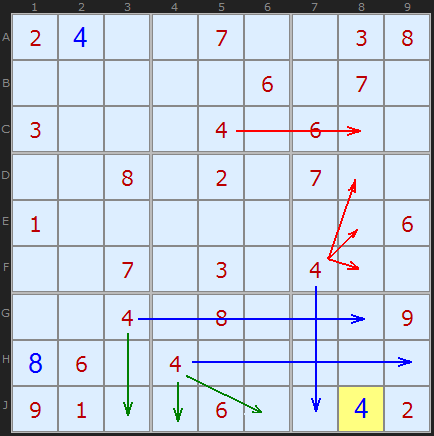
Sometimes there are several reasons for a placement. This four in J8 is a great example. In blue I have shown that 4 in J8 is the last remaining number in terms of the box it is in. The red lines (plus blue lines) show it is the last number in column 8 and the green lines demonstrate it is the last number in row J.

This 4 has been pinned to the board quite conclusively. 		Last number in row, columns and box
Last number in row, columns and box
The Last Possible Number

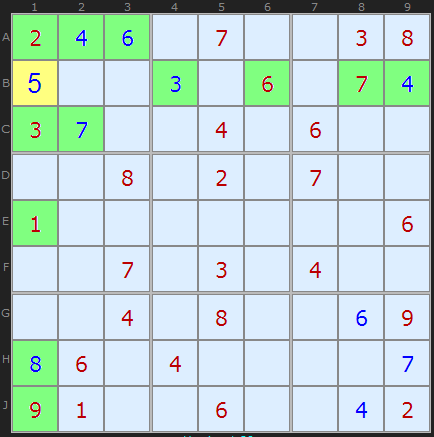
Eyeballing is actually quicker than checking each cell for the last possible number, but it is a valid approach, so I include it here. It is the sort of strategy a beginner thinks of when faced with the puzzle for the first time. It is best used when a cell stands out because all the other numbers seem to be in place.

Here the 5 in B1 can be determined because every other number from 1 to 9 apart from 5 is present in either the row, column or box (marked in green).
 The Last Possible Number
The Last Possible Number
In the jargon, this is a Naked Single - if you were using candidates at this stage it would be the only candidate in the cell. The 'eyeballing' techniques help determine Hidden Singles since other candidates are possible in those places but at least one candidate is unique to a particular row, column and box. You can see this difference if you 'take step' with candidates turned on.



Continue to Naked Candidates



  
   
Comments

Your Name/Handle

Email Address - required for confirmation (it will not be displayed here)

Your comment or question

Please enter the
letters you see:
arrow		Enter these letters Remember me


Please keep your comments relevant to this article.
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted — no need to use <p> or <br> tags.


Comments - Talk

Wednesday 13-Feb-2013

... by: Mike

I enjoy doing the puzzles in the newspaper
I got bord with the Jumble so I moved on to the
celebrity cipher and mastered that one .My brother got me started with Sudoku and its really a
challenge .Just started it last week. I think the eyeballing is a good way to start. great web
site, keep up the good work.

Mike

Sunday 13-Jan-2013

... by: Anon

After years of struggle, I decided to go to basics - and used my "eyeball". Thank you for this piece.

Tuesday 8-Jan-2013

... by: Amir Latif

I developed something I call an "Index." You make a list of all the numbers NOT appearing in a column, or row, or even a square. Test the index against each blank position in the column. If you get a match in the neighbourhood for each number in the index but one, that number goes in the blank cell. The "neighbourhood" includes the contents of the row, column and square that that blank cell is in,
It may not always work, and often you may have to do some manual testing.

Please tell me that other people are using this device which came to me.
Blessings, Amir

Monday 7-Jan-2013

... by: cliff

Getting started really made the puzzle simplier I love this puzzle its a great
brain teaser

Tuesday 20-Nov-2012

... by: ly ousmane

it's my 1st time and i have no clue whatsoever of solving it,don't even know where to start.

Friday 27-Apr-2012

... by: Satish Gupta

It is the best thing I have seen about sudoku which I got exposed to about 10 days ago

 Post a Comment using Facebook...


Article created on 25-January-2012. Views: 57085
This page was last modified on 14-April-2012, at 00:00.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Syndicated Puzzles Inc, 2012