A Set Theory Approach to Sudoku Strategies
Abstract: 'Generalizing Sudoku Strategies'

This paper seeks to define a smaller set of more generalized strategies, which make the relationship among some of the named strategies more explicit, suggest other strategies for solving puzzles, and offer a path to simplify Sudoku solvers.
Using set notation, this paper defines six generalized strategies which encompass sixteen or more individual strategies. These generalized strategies may be implemented in computerized algorithms.
The paper concludes with some thoughts on ranking puzzle difficulty, and on open questions involving the completeness and efficiency of Sudoku solution strategies.
by Kevin Gromley, March 2014
This is a fascinating paper by Kevin Gromley who has set out a way to group families of logical strategies based on 'constraint sets'. I'm not nearly mathematical enough to appreciate the set theory formulas but we have exchanged ideas about the conclusions of this paper and discussed some of the open questions. I'd like to pick out a few points and write about them here.
- Firstly, it's worth re-iterating what a 'logical' Sudoku strategy really *is*. The strategies on this site are dominated by what I called 'pattern' based logic - that there is a pattern in the candidates on the board and we can make a deduction about some of the numbers that leads to candidates being removed and cells solved. Kevin has coined the excellent term State Deterministic to say the same thing and I'm completely won over by this term. From the initial puzzle the state of the board as it exists determines the next state - and through a series of steps we take the puzzle through to the solution.
I contrast this with strategies that require you to change the board and see what happens. So called 'trial and error strategies' like "if that cell was a 3, does it work out or not". These can be applied in a logical and rational way so in a weak sense it is 'logical' but most solvers would agree that it is akin to guessing and much less elegant. - Before my discussion with Kevin I was of the belief that for logical strategies to work on a puzzle the puzzle has to have a unique solution. This is true but there is in fact a stronger relationship between uniqueness and logic. Because State Deterministic strategies are subtractive in nature a puzzle solved in this way means that we have *proved* the puzzle has a unique solution. This is an important point because a guessing strategy can never prove a single solution unless it exhaustively tests every value in every cell. The brute-force 'Solution Count' does this in extremis.
So if we cannot solve a puzzle using State Deterministic strategies either the puzzle is faulty or we don't have enough strategies. Kevin's work has set out proofs using constraint sets that envelope a large number of strategies proposed on this site. That is impressive but some puzzle solutions are still out of reach using only those tools. Nevertheless, it holds out hope that we can solve all puzzles using these methods. I see many complex and interesting solutions on the Weekly Unsolveables Puzzles that show a state deterministic solution on an individual basis.
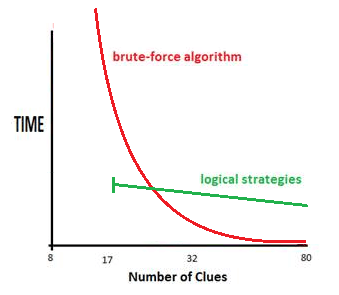
- Another point the paper discussed was the efficiency of the strategies. For a given Sudoku puzzle, is there an a priori way to determine or estimate an efficient set of rules to apply? On one hand this is a very practical question since I am very interested in optimizing solving algorithms. It takes time to test a large set of difficult puzzles. But this question is bound up with the notion that there are many paths to solving a puzzle even though there is only one start position (the puzzle) and one end position (the solution). It may not matter to the pen and paper solver whether their solution is the best solution - but does State Determinism tell us anything about the *best* and *shortest* solve path? Without exhaustively testing all paths?
I knocked up a quick graph to show the very rough relationship between logical strategies and brute-force - the two competing approaches to finding solutions. Brute Force is incredibly fast at high numbers of clues. I've dropped in 17 as the minimum number of clues on a normal Sudoku - my implementation can take a few seconds on these puzzles. The 8 is the smallest number of clues in a Jigsaw Sudoku - expotentialism takes over and I've never waited long enough to see how long it takes.
The straight green line should be a rather hazy line because clue density has almost no bearing on the complexity of the puzzle except in the gross sense of less or more availability for steps. There are trivial 17 clue puzzles and horrendous 30 clue ones. But logical strategies only take 5-10 seconds on the hardest puzzles and so the time spread is fairly flat.
- Andrew Stuart

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Adam Mitchneck
At its core, logical proofs are based on the logic that the statement (A or not A) is always true (which will be the case, unless the puzzle has no solution, in which case it is invalid and not part of this discussion). When solving a Sudoku puzzle, we take a piece of paper and draw one line down the middle and one across the top to create a header row. In this header, on the left side, we make a statement like "cell A1 is a 3". On the right side, we make the inverse statement "cell A1 cannot be 3". The makes the left statement "A" and the right statement "not A". We then continue down each side adding statements based on the logic "if A then B." For instance, if cell A1 is 3, then cell A7 cannot be 3, allowing us the add "A7 cannot be 3" to the left side of our proof. Note that the Single-S, Two-S, and Multi-S Strategies mentioned in the paper can all be used within proofs to add statements to either side. Additionally, further logic proofs can be used on either side to create more statements on that side.
When both the right and left side of the proof share a statement "B", such as "cell D5 cannot be 7", then this statement is true for the puzzle being solved by the proof (or, in a case where the proof is used on the right or left side of another proof, this statement can be added to that side of the underlying proof). This is proven by the logic "if (A or not A) then B"; since "A or not A" is logically true, B logically must also be true.
Another possibility is for the right or left side of the proof to result in nil, meaning that it requires more than one number to exist within the same cell at the same time or does not allow any number to exist within some cell. In this case, the proof indicates that the initial statement on that side was false, meaning the inverse statement, along with its inferred statements, must be true.
... by: Anonymous
... by: Nat Sothanaphan
The idea, in non-mathematical terms, is as follows:
Consider a "bent subset" that spread over a box and a row/column. Let A be the part of the subset inside the intersection, B and C the parts outside the intersection.
A A . | . B . | . . .
. C . | . . . | . . .
. . . | . . . | . . .
Then
(1) If B and C have no value in common, then
a) every value in B can be eliminated from every cell seeing that value in the subset.
b) every value in C can be eliminated from every cell seeing that value in the subset.
(2) If B and C have exactly 1 value in common, then that value can be eliminated from every cell seeing that value in the subset.
The proof of this is that if said value is ON, the "bent subset" will be reduced to a set containing fewer values than cells, and with B and C having no value in common. Because B and C has no value in common, it can be "bent" back into an equivalent normal subset which has fewer values than cells, which is a contradiction.
This is definitely a natural progression from Y-wing, XYZ-wing (3 cells) and WXYZ-wing (4 cells) to arbitrary number of cells. To see its potential, see how it solves all examples in the APE page (Example 1 and 4 are just Y-wing and XYZ-wing):
Example 2:
A1, B3, C2, C9 form a bent subset {1,3,7,8}
{A1, B3} and {C9} have only 3 in common.
Therefore every cell that sees every 3 in subset, C3 cannot contain 3.
Example 3:
A1, A3, C1, C3, H3 form a bent subset {1,4,5,7,9}
{A1,C1} and {H3} have only 7 in common.
Therefore every cell that sees every 7 in subset, B3 cannot contain 7.
Example 5:
B8, B9, C1, C3, C7 form a bent subset {1,4,5,7,9}
{B8, B9} and {C1, C3} have only 1 in common.
Therefore every cell that sees every 1 in subset, B1 cannot contain 7 (and also B2 and C9! If you use APE, you have to use it three times).
Example 6:
A3, B1, D3, E3, F3 form a bent subset {1,3,4,6,7}
{B1} and {D3, E3, F3} have only 6 in common.
Therefore every cell that sees every 6 in subset, D1 cannot contain 6.
Eight-cell Example:
I like the idea of using 8 cells simultaneously. But, with bent subset, we need to use only five cells:
B5, C5, D5, D6, E6 form a bent subset {1,2,6,7,9} (This is like WXYZ-wing in the narrow definition but with five cells)
{B5, C5} and {D6, E6} have only 2 in common.
Therefore, every cell that sees every 2 in subset, E5 cannot contain 2.
I believe this is the generalization of all Wing theories we are looking for!