XY-Chains

XY-Chains is a way to connect two parts of the board that can't directly "see" each other. The "X" and the "Y" in the name represent these two values in each chain link. If we can connect the ends we can make deductions.

Originally these were found by extending Y-Wings into so-called Y-Wing Chains but it was quickly transformed into this more encompassing strategy. The same pincer-like attack on candidates that both ends can see by chaining bi-value cells. With Y-Chains the hinge relied on identical bi-value cells but in an XY-Chain the candidate can differ by one on each hop.

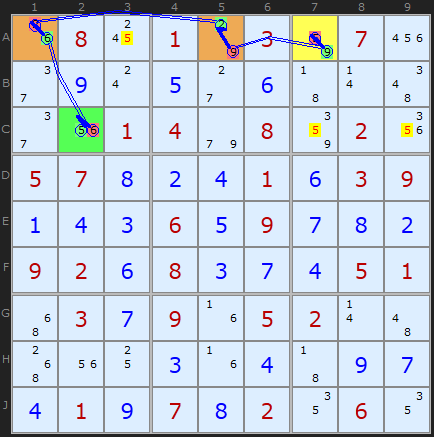
The example here is a very simple XY-Chain of length 4 which removed all 5's highlighted in yellow. The chain ends are 5 A7 and C2 - so all cells that can see both of these are under fire. It's possible to start at either end but lets follow the example from A7. We can reason as follows

• If A7 is 5 then A3/C7/C9 cannot be.
  
• if A7 is NOT 5 then it's 9, so A5 must be 2, which forces A1 to be 6. If A1 is 6 then C2 is 5.
  

Which ever choice in A7 the 5's in A3/C7/C9 cannot be 5. The same logic can be traced from C2 to A7 so the strategy is bi-directional, in the jargon.

The solver uses relatively simple chain notation with cells identified with [Row Letter+Column]. (There is an option to change to rYcX coordinates). In a chain we're alternating between strong and weak links but also turning candidates ON and OFF. To symbolise that the chain uses plus and minus. The number being turned on or off follows the symbol. The above example is
-5[A7]+9[A7]-9[A5]+2[A5]-2[A1]+6[A1]-6[C2]+5[C2]
5 taken off A3
5 taken off C7
5 taken off C9

In later documentation on Grouped X-Cycles you will see grouped cells denoted as +4[D4|E4] and when ALSs are used to make a link curly brackets are used: +7{H6|G6}. Rare exotic links like Unique Rectangles are named -9(UR[DF28]) as is an X-Wing -8(XW[-E3/-B3+B2-E2])

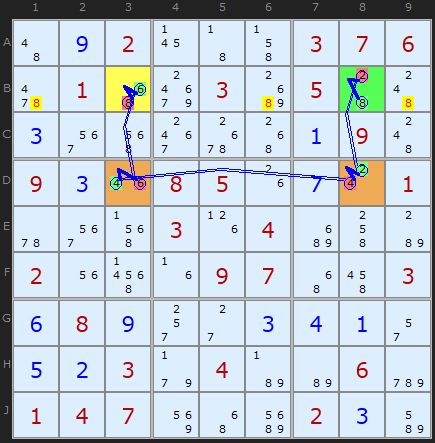
This next Sudoku puzzle contains an entertaining series of XY-Chains, starting with this rectangular one. It proves that 8 must be in either B3 or B8 and therefore we can remove the other three 8s in row B. Starting on B3 if that cell is either 8 or 6. If it is 6 then D3 must be 4 which pushes 2 into D8 which in turn makes B8 8. You can trace this from B8 back round for the same effect. A nice short XY-Chain, but as the next example shows, these four cells are a rich seam.

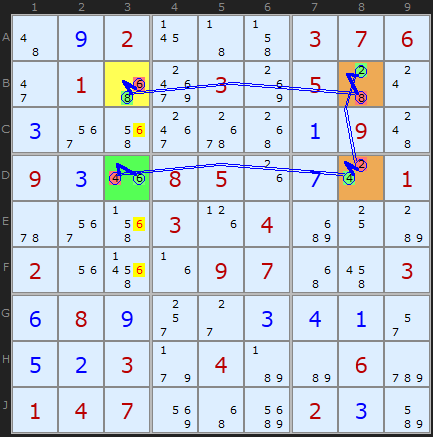
(Uncheck Rectangle Elimination)

Looking at exactly the same starting cell it appears we can make further eliminations, this time 6s in column 3. We go clock-wise, this time, round the rectangle. It proves 6 will either be on B3 or D3.

If you want to finish the puzzle by yourself, look out for a third elimination with those same four cells using 2s on column 8, or step through with the solver.

XY-Chains Exemplars

These puzzles require the XY-Chains strategy at some point but are otherwise trivial.
They also require one Naked Pair (except for #5).
They make good practice puzzles.

• Exemplar 1, x1 (score 81)
• Exemplar 2, x1 (score 82)
• Exemplar 3, x4 (score 113)
• Exemplar 4, x4 (score 115)
• Exemplar 5, x9 (score 307) - OMG! 9 chains!

Thanks to Klaus Brenner for number 5