With X-Wings we looked at a rectangle formed by four numbers at the corners. This allowed us to exclude other occurrences of that number in either the row or column. We can extend this pattern to nine cells and achieve even more eliminations.

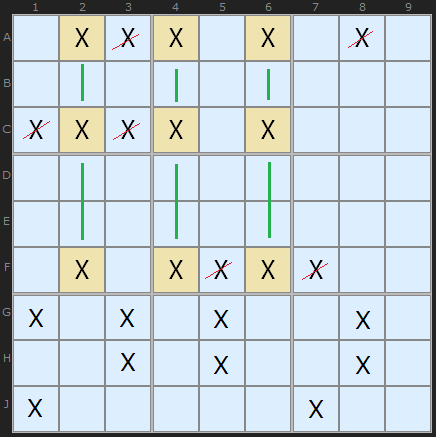
A Sword-Fish is a 3 by 3 nine-cell pattern where a candidate is found on three different rows (or three columns) and they line up in the opposite direction. Eventually we will fix three candidates somewhere in those cells which excludes all other candidates in those units. The shaded cells show the Sword-Fish where X is unique to three cells in columns 2, 4 and 6. They are aligned on rows A, C and F. This means we can remove all candidate X in the other positions on those rows.

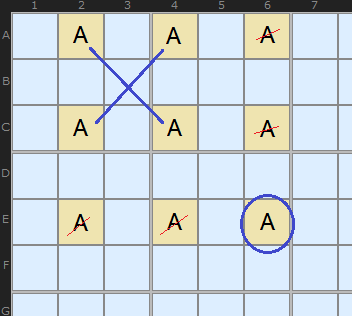
If you are not convinced that the shaded cells really must contain the solutions we can argue this way. All Sword-Fishes will break down into X-Wings and because we know X-Wings work, so will the Sword-Fish. Take this arrangement of candidate A and let’s pretend that E6 is the solution. We ‘remove’ the rest of A in column 6 and row E. That leaves a X-Wing in AC24.

X-Wing inside a Sword-Fish

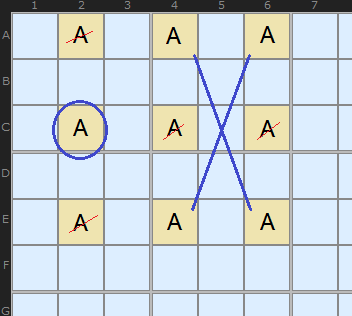
If that works for E6, let’s try another cell. Pretending C2 is a solution we remove the rest of A in row C and column 2. Again we get an X-Wing. So all cells in the 3 by 3 grid are ‘locked’ together.

Another way to cut it

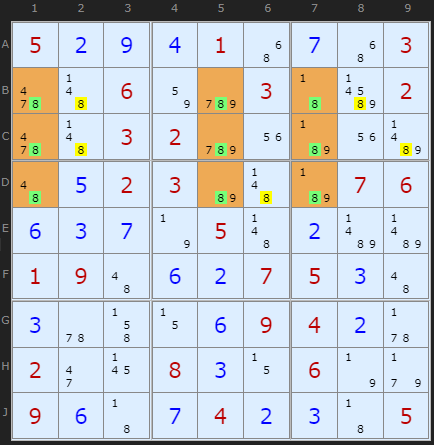
To match theory with practise the first example is a perfect 3-3-3 Swordfish, so called because all three candidates in each column are present (that is, no solved 8s in the pattern). The yellow cells are the Swordfish cells. The green cells are those cells where 8 can be removed. A perfect Sword-Fish is extremely rare. This one is provided by Klaus Brenner who found it in the newspaper La Libre Belgique.

Perfect 3-3-3 Swordfish: Load Example or : From the Start

If you remember how Naked and Hidden Triples work you'll remember that they require three numbers in three cells - in total. It's not necessary for every number to be in all three cells. So it is with the Sword-Fish.

Swordfishes come in a number of variations depending on the number of X present in the nine cells that make up a Swordfish. With an X-Wing you need candidate X in all four cells of the 2 by 2 formation, but with the 3 by 3 Swordfish formation you don't need X in every cell - just as long as it is spread out over 3 by 3 cells. The next example has 9 twice in each row and is called a 2-2-2 Swordfish.

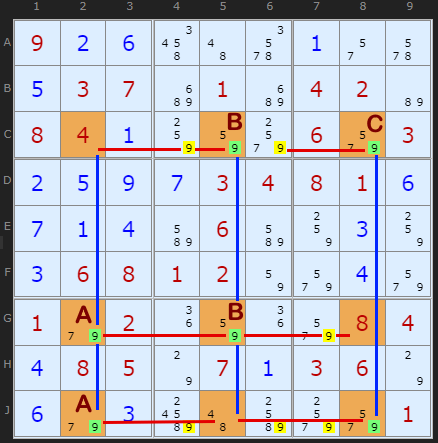
This is a 2-2-2 formation Sword-Fish. It reduces to three pairs which I have labelled AA, BB and CC. Notice how they are staggered so that they still cover three columns. This is a minimal Sword-Fish but it does the job. We have six 9s that can go in one swoop.

Swordfish Example 1: Load Example or : From the Start

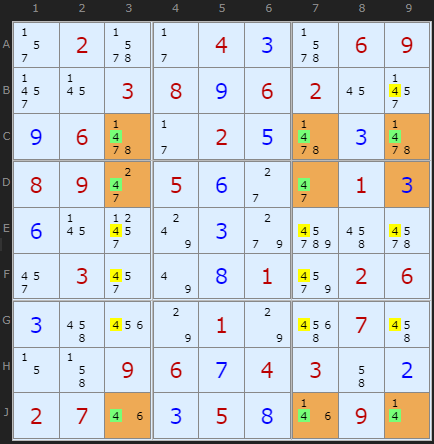
This second Sword-Fish is orientated in the opposite direction and we eliminate in the columns. A Sword-Fish can be referred to by combining the row and columns numbers, which makes this example CDJ379. In formation terms it is 3-2-3.

Sword-Fish example 2: Load Example or : From the Start