There are two major types of Multi-colouring and neither are for the faint hearted.
You'll need four coloured pencils ;-)
Fortunately we are only scanning the board for single numbers in conjugate pairs. These occur where a candidate exists only twice in any row, colum or box (unit). We can chain these togther if there are sufficient numbers of them just as we did for simple colouring above. In Multi-Colouring we are looking for two or more chains. It is important they don't link up - three or more appearances of the candidate number in an intervening unit prevent the 'link up' of two chains.

Given two chains we can label them A and B. A+ and A- will indicate the alternating states so that EITHER all of A+ are true OR all of A- are true. We don't know which way round yet. Similarly B+ and B- indicate alternating true/false for that chain. C+ and C- continues the theme if there are more chains on the same candidate number. Give A+, A-, B+ and B- we can colour them on the board to see the patterns.

Type 1 Multi-Colouring
The Rule is as follows: If A+ shares a unit with B+ and B- then A+ must be the false candidate since either B+ or B- must be true.

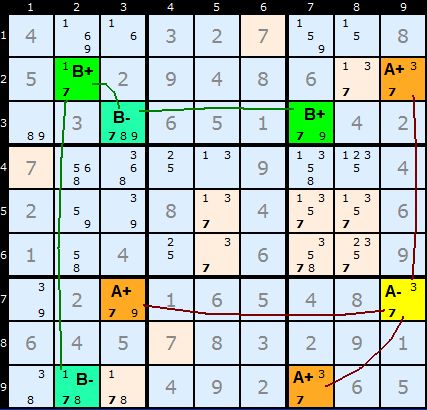
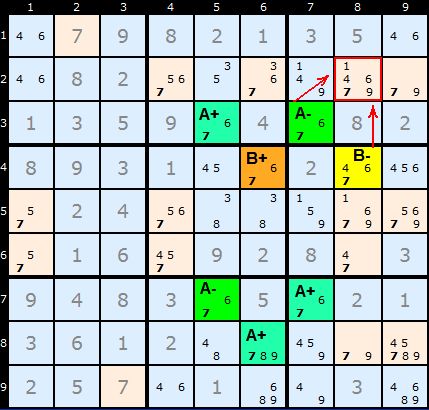
In this Sudoku we've looking at number 7 and labelled two chains A and B and settled on the plus and minus symbols. I have labelled them so that they match the rule. (Don't make a category mistake and think the rule applies just because you've assigned the lables!). Now, the yellow cell marked A- does not share a unit with any of B cells. However, all three cells marked A+ can see a B+ or a B- in one or more shared units. Since the solution cannot be both B+ and B- but must be at least all of B+ or all of B- every cell in A+ must be false and number 7 can be removed from all A+ cells.

Multi-Colouring Type 1 eg 1: Load Example or : From the Start

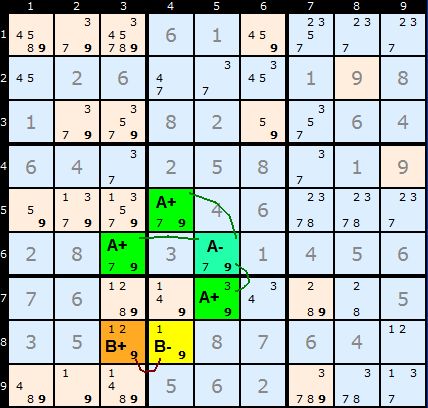
This second example is provided to illustrate the idea a bit further. A+ is again the victim and all the labels are the same as the first example. It also shows that the chains can be quite short. Interestingly, although B can be a chain of just two cells A must be a longer chain. Otherwise we'd be in a situation where the Sudoku has two solutions or multi-colouring can be reduced to a Unique Rectangle.

Multi-Colouring Type 1 eg 2: Load Example or : From the Start

Type 2 Multi-Colouring

If A+ shares a unit with B+ then any cell with the given candidate and sharing a unit with both A- and B- can have that candidate excluded. The Reason: Since A+ and B+ can't both be true, then either one or both of A- and B- must be true. Therefore any cell sharing a unit with both A- and B- can safely have that candidate excluded.

This is a bit of a mouthful. What we're looking at are cells marked A+ which can see B+ cells but A- cells cannot see B- cells. A+ and B+ both can't be true since they share units in two cases. One or perhaps both of the units marked A- and B- must be true. All cells that can see an A- and a B- can't contain the candidate, in this example number 8. In R3C5 an 8 can see R2C4 AND R8C5. Similarly the 8 in R7C4 can see R2C4 and R8C5/R7C9.

Multi-Colouring Type 2, Example 1: Load Example or : From the Start

This smaller example might be more easy to understand. The labels are the same so that one A+ can see a B+. There is just one place where a 7 is at the overlap of an A- and a B-.

Multi-Colouring Type 2 eg 2: Load Example or : From the Start

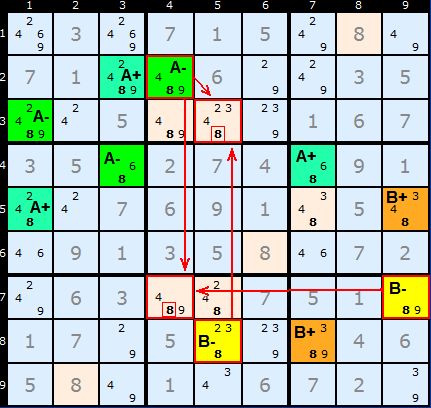
Multi-Colouring with 3+ chains

I don't have an example of a Sudoku requiring a multi-colouring solution using three or more chains.
I'd be very grateful for an example.